2.2 如何画一个圆
圆的方程由以下定义:
x^2 + y^2 = r^2
x = x-coordinate on graph
y = y-coordinate on graph
r = radius of circle
我们可以重新排列变量,使方程等于零:
x^2 + y^2 - r^2 = 0
要在图表上可视化这一点,您可以使用 Desmos calculator绘制以下内容:
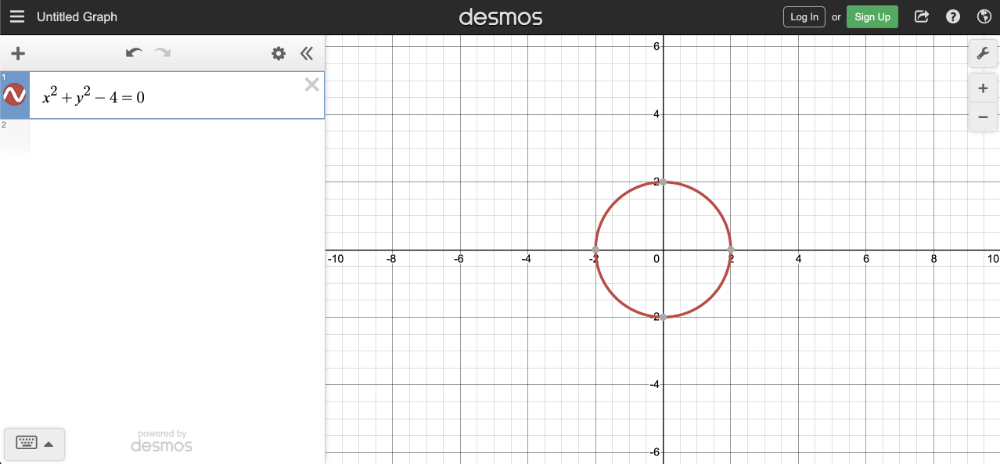
x^2 + y^2 - 4 = 0
如果复制上述代码段并将其粘贴到 Desmos calculator= 中,那么您应该会看到一个半径为 2 的圆的图形。圆心位于坐标 (0, 0) 处。
在 Shadertoy 中,我们可以使用这个方程的左侧 (LHS) 来画一个圆。让我们创建一个名为 sdfCircle 的函数,该函数返回 XY 坐标处每个像素的颜色 white,以便方程大于 0,否则返回颜色 blue。
该函数的 sdf 部分引用了一个称为有符号距离函数 (SDF) 的概念,也称为有符号距离场。在 3D 中绘制时,使用 SDF 更为常见,但我也会将这个术语用于 2D 形状。
我们将在 mainImage 函数中调用新函数来使用它。
vec3 sdfCircle(vec2 uv, float r) {
float x = uv.x;
float y = uv.y;
float d = length(vec2(x, y)) - r;
return d > 0. ? vec3(1.) : vec3(0., 0., 1.);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord/iResolution.xy; // <0,1>
vec3 col = sdfCircle(uv, .2); // Call this function on each pixel to check if the coordinate lies inside or outside of the circle
// Output to screen
fragColor = vec4(col,1.0);
}
如果你想知道我为什么使用 0. 而不是简单地用 0 来代替没有小数点的 0,这是因为在整数的末尾添加一个小数会使它成为 float 而不是 int 的类型。当您使用需要 float 类型数字的函数时,将小数放在整数的末尾是满足编译器要求的最简单方法。
我们使用的半径为 0.2,因为我们的坐标系设置为仅具有介于 0 和 1 之间的 UV 值。当你运行代码时,会注意到似乎有些错误。
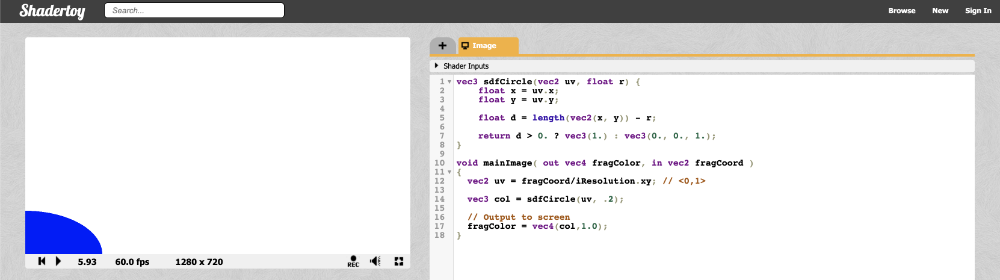
画布的左下角似乎有四分之一的蓝色的圆。为什么?因为我们的坐标系当前设置为原点在左下角。我们需要将每个值移动 0.5 以�获得画布中心坐标系的原点。
从 UV 坐标中减去 0.5:
vec2 uv = fragCoord/iResolution.xy; // <0,1>
uv -= 0.5; // <-0.5, 0.5>
现在,x 轴和 y 轴的范围都介于 -0.5 和 0.5 之间,这意味着坐标系的原点位于画布的中心。然而,我们面临另一个问题......
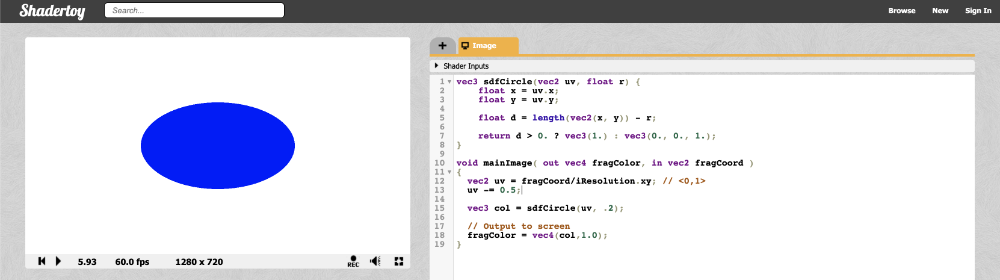
我们的圆看起来有点拉长,所以它看起来更像一个椭圆。这是由画布的纵横比引起的。当画布的宽度和高度不匹配时,圆圈将显示为拉伸。我们可以通过将 UV 坐标的 X 分量乘以画布的纵横比来解决此问题。
vec2 uv = fragCoord/iResolution.xy; // <0,1>
uv -= 0.5; // <-0.5, 0.5>
uv.x *= iResolution.x/iResolution.y; // fix aspect ratio
这意味着 X 分量不再介于 -0.5 和 0.5 之间。它将在与画布的纵横比成比例的值之间移动,而纵横比将由浏览器或网页的宽度决定(如果您使用 Chrome DevTools 之类的工具来更改宽度)。
你完成的代码应如下所示:
vec3 sdfCircle(vec2 uv, float r) {
float x = uv.x;
float y = uv.y;
float d = length(vec2(x, y)) - r;
return d > 0. ? vec3(1.) : vec3(0., 0., 1.);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord/iResolution.xy; // <0,1>
uv -= 0.5;
uv.x *= iResolution.x/iResolution.y; // fix aspect ratio
vec3 col = sdfCircle(uv, .2);
// Output to screen
fragColor = vec4(col,1.0);
}
运行代码后,您应该会看到一个完美比例的蓝色圆圈!🎉
请注意,这只是给圆圈着色的一种方式。我们将在本教程系列的第 4 部分中学习另一种方法。它将帮助我们在画布上绘制多个形状。
我们可以从中获得一些乐趣!我们可以使用全局 iTime 变量来随时间更改颜色。通过使用余弦 (cos) 函数,我们可以一遍又一遍地循环显示同一组颜色。由于余弦函数在值 -1 和 1 之间振荡,因此我们需要将此范围调整为 0 到 1 之间的值。
请记住,最终片段颜色中任何小于零的颜色值都将自动固定为零。同样,任何大于 1 的颜色值都将被限制为 1。通过调整范围,我们可以获得更广泛的颜色范围。
vec3 sdfCircle(vec2 uv, float r) {
float x = uv.x;
float y = uv.y;
float d = length(vec2(x, y)) - r;
return d > 0. ? vec3(0.) : 0.5 + 0.5 * cos(iTime + uv.xyx + vec3(0,2,4));
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord/iResolution.xy; // <0,1>
uv -= 0.5;
uv.x *= iResolution.x/iResolution.y; // fix aspect ratio
vec3 col = sdfCircle(uv, .2);
// Output to screen
fragColor = vec4(col,1.0);
}
运行代码后,您应该会看到圆圈在各种颜色之间发生变化。

您可能会对 uv.xyx 中的语法感到困惑。这称为 Swizzling。我们可以使用变量的分量创建新的向量。让我们看一个例子。
vec3 col = vec3(0.2, 0.4, 0.6);
vec3 col2 = col.xyx;
vec3 col3 = vec3(0.2, 0.4, 0.2);
在上面的代码片段中,col2 和 col3 的值是相同的。