9.2 鼠标输入
Shadertoy 提供了一组全局变量,您可以在着色器代码中使用这些变量,以使其更具交互性。如果您打开一个新的着色器并单击Shader inputs旁边的箭头,那么您��将看到一个全局变量列表。
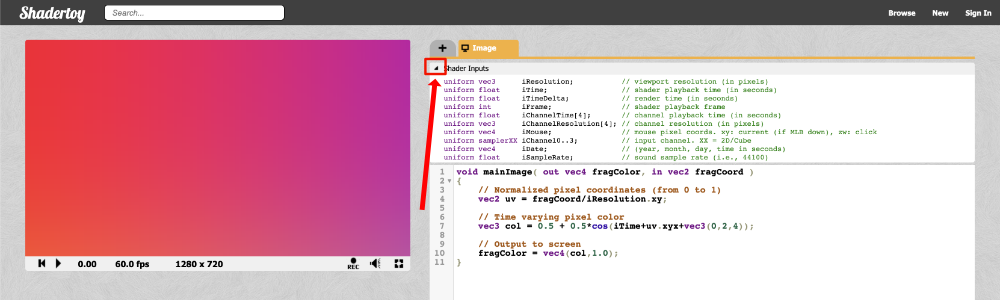
下面是您可以在 Shadertoy 着色器中使用的全局变量列表。
// Shader Inputs
uniform vec3 iResolution; // viewport resolution (in pixels)
uniform float iTime; // shader playback time (in seconds)
uniform float iTimeDelta; // render time (in seconds)
uniform int iFrame; // shader playback frame
uniform float iChannelTime[4]; // channel playback time (in seconds)
uniform vec3 iChannelResolution[4]; // channel resolution (in pixels)
uniform vec4 iMouse; // mouse pixel coords. xy: current (if MLB down), zw: click
uniform samplerXX iChannel0..3; // input channel. XX = 2D/Cube
uniform vec4 iDate; // (year, month, day, time in seconds)
uniform float iSampleRate; // sound sample rate (i.e., 44100)
其中,您将看到一个名为 iMouse 的变量,当您单击画布上的某个位置时,该变量可用于获取鼠标的位置。此变量的类型为 vec4,因此包含有关鼠标左键单击的四条信息。
vec4 mouse = iMouse;
mouse.xy = mouse position during last button down
abs(mouse.zw) = mouse position during last button click
sign(mouze.z) = button is down (positive if down)
sign(mouze.w) = button is clicked (positive if clicked)
鼠标单击是按下鼠标后立即发生��的情况。鼠标按下事件是继续按住鼠标后发生的情况。
Shadertoy 的共同创建者之一 Inigo Quilez 编写的教程向您展示了如何使用 iMouse 中存储的每条数据。单击场景中的任意位置时,单击鼠标时会显示一个白色圆圈。如果您继续按住鼠标并四处移动鼠标,两个圆圈之间会出现一条黄线。松开鼠标后,黄线将消失。
在本教程中,我们真正关心的是鼠标坐标。我做了一个小演示来演示如何使用鼠标在画布中移动圆圈。让我们看看代码:
float sdfCircle(vec2 uv, float r, vec2 offset) {
float x = uv.x - offset.x;
float y = uv.y - offset.y;
float d = length(vec2(x, y)) - r;
return step(0., -d);
}
vec3 drawScene(vec2 uv, vec2 mp) {
vec3 col = vec3(0);
float blueCircle = sdfCircle(uv, 0.1, mp);
col = mix(col, vec3(0, 1, 1), blueCircle);
return col;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord/iResolution.xy - 0.5; // <-0.5,0.5>
uv.x *= iResolution.x/iResolution.y; // fix aspect ratio
// mp = mouse position of the last click
vec2 mp = iMouse.xy/iResolution.xy - 0.5; // <-0.5,0.5>
mp.x *= iResolution.x/iResolution.y; // fix aspect ratio
vec3 col = drawScene(uv, mp);
// Output to screen
fragColor = vec4(col,1.0);
}
请注意,获取鼠标位置与 UV 坐标非常相似。我们可以通过以下语句对坐标进行归一化:
vec2 mp = iMouse.xy/iResolution.xy // range is between 0 and 1
这会将鼠标坐标标准化为介于 0 和 1 之间。通过减去 0.5,我们可以将鼠标坐标标准化为 -0.5 到 0.5 之间。
vec2 mp = iMouse.xy/iResolution.xy - 0.5 // range is between -0.5 and 0.5
使用鼠标平移摄像机
现在我们了解了如何使用 iMouse 全局变量,让我们将其应用于我们的相机。我们可以使用鼠标通过更改光线原点 ro 的值来控制平移。
vec2 mouse = iMouse.xy / iResolution.xy - 0.5; // <-0.5,0.5>
vec3 ro = vec3(mouse.x, mouse.y, 3); // ray origin will move as you click on the canvas and drag the mouse
如果您单击画布并拖动鼠标,您将能够在 x 轴和 y 轴上在 -0.5 到 0.5 之间平移摄像机。画布的中心将是点 (0, 0),它应该将立方体移回画布的中心。
如果要平移更多,您始终可以将鼠标位置值乘以乘数。
vec2 mouse = iMouse.xy / iResolution.xy - 0.5; // <-0.5,0.5>
vec3 ro = vec3(2. * mouse.x, 2. * mouse.y, 3);

使用鼠标倾斜/旋转摄像机
我们可以通过更改 theta 的值来使用鼠标倾斜/旋转相机,theta 是我们提供给旋转矩阵的角度,例如 rotateX、rotateY 和 rotateZ。确保您不再使用鼠标来控制光线原点 ro。否则,您最终可能会得到一个非常奇怪的相机。
让我们对光线方向应用倾斜,以从左向右倾斜摄像机。
vec2 mouse = iMouse.xy / iResolution.xy - 0.5; // <-0.5,0.5>
vec3 rd = normalize(vec3(uv, -1)); // ray direction
rd *= rotateY(mouse.x); // apply yaw
由于 mouse.x 当前限制在 -0.5 和 0.5 之间,因此将此范围重新映射到负 pi (-π) 到正 pi (+π) 可能更有意义。要将范围重新映射到新范围,我们可以使用 mix 函数。它已经构建为处理线性插值,因此非常适合将值从一个范围重新映射到另一个范围。
让我们将范围<-0.5,0.5>重新映射到<-π,π>。
vec2 mouse = iMouse.xy / iResolution.xy - 0.5; // <-0.5,0.5>
vec3 rd = normalize(vec3(uv, -1)); // ray direction
rd *= rotateY(mix(-PI, PI, mouse.x)); // apply yaw with a 360 degree range
现在,我们可以使用鼠标进行完整的 360 度旋转!
您可能想知道如何使用 mouse.y 值。我们可以使用此值将摄像机作为 pitch 角度上下倾斜。这意味着我们需要利用 rotateX 函数。
vec2 mouse = iMouse.xy / iResolution.xy - 0.5; // <-0.5,0.5>
vec3 rd = normalize(vec3(uv, -1)); // ray direction
rd *= rotateX(mouse.y); // apply pitch
这将允许我们在 -0.5 和 0.5 的值之间上下倾斜摄像机。
如果你想用鼠标同时改变 mouse.x 的 yaw 角度和 mouse.y 的 pitch 角度,那么我们需要将旋转矩阵相乘。
vec2 mouse = iMouse.xy / iResolution.xy - 0.5; // <-0.5,0.5>
vec3 rd = normalize(vec3(uv, -1));
rd *= rotateY(mouse.x) * rotateX(mouse.y); // apply yaw and pitch
现在,您可以用鼠标自由倾斜相机来环顾场景!这对于对使用 Shadertoy 构建的复杂 3D 场景进行故障排除非常方便。在 Unity 或 Blender 等软件中,您已经拥有了一台功能强大的相机,可以使用它来查看 3D 场景。
您可以在下面找到完成的代码:
// Rotation matrix around the X axis.
mat3 rotateX(float theta) {
float c = cos(theta);
float s = sin(theta);
return mat3(
vec3(1, 0, 0),
vec3(0, c, -s),
vec3(0, s, c)
);
}
// Rotation matrix around the Y axis.
mat3 rotateY(float theta) {
float c = cos(theta);
float s = sin(theta);
return mat3(
vec3(c, 0, s),
vec3(0, 1, 0),
vec3(-s, 0, c)
);
}
// Rotation matrix around the Z axis.
mat3 rotateZ(float theta) {
float c = cos(theta);
float s = sin(theta);
return mat3(
vec3(c, -s, 0),
vec3(s, c, 0),
vec3(0, 0, 1)
);
}
// Identity matrix.
mat3 identity() {
return mat3(
vec3(1, 0, 0),
vec3(0, 1, 0),
vec3(0, 0, 1)
);
}
const int MAX_MARCHING_STEPS = 255;
const float MIN_DIST = 0.0;
const float MAX_DIST = 100.0;
const float PRECISION = 0.001;
struct Surface {
float sd; // signed distance value
vec3 col; // color
int id; // identifier for each surface/object
};
/*
Surface IDs:
1. Floor
2. Box
*/
Surface sdBox( vec3 p, vec3 b, vec3 offset, vec3 col, mat3 transform)
{
p = (p - offset) * transform;
vec3 q = abs(p) - b;
float d = length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0);
return Surface(d, col, 2);
}
Surface sdFloor(vec3 p, vec3 col) {
float d = p.y + 1.;
return Surface(d, col, 1);
}
Surface minWithColor(Surface obj1, Surface obj2) {
if (obj2.sd < obj1.sd) return obj2;
return obj1;
}
Surface sdScene(vec3 p) {
vec3 floorColor = vec3(.5 + 0.3*mod(floor(p.x) + floor(p.z), 2.0));
Surface co = sdFloor(p, floorColor);
co = minWithColor(co, sdBox(p, vec3(1), vec3(0, 0.5, -4), vec3(1, 0, 0), identity()));
return co;
}
Surface rayMarch(vec3 ro, vec3 rd, float start, float end) {
float depth = start;
Surface co; // closest object
for (int i = 0; i < MAX_MARCHING_STEPS; i++) {
vec3 p = ro + depth * rd;
co = sdScene(p);
depth += co.sd;
if (co.sd < PRECISION || depth > end) break;
}
co.sd = depth;
return co;
}
vec3 calcNormal(in vec3 p) {
vec2 e = vec2(1.0, -1.0) * 0.0005; // epsilon
return normalize(
e.xyy * sdScene(p + e.xyy).sd +
e.yyx * sdScene(p + e.yyx).sd +
e.yxy * sdScene(p + e.yxy).sd +
e.xxx * sdScene(p + e.xxx).sd);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = (fragCoord-.5*iResolution.xy)/iResolution.y;
vec3 backgroundColor = vec3(0.835, 1, 1);
vec3 col = vec3(0);
vec3 ro = vec3(0, 0, 3); // ray origin that represents camera position
vec2 mouse = iMouse.xy / iResolution.xy - 0.5; // <-0.5,0.5>
vec3 rd = normalize(vec3(uv, -1)); // ray direction
rd *= rotateY(mouse.x) * rotateX(mouse.y); // apply yaw and pitch
Surface co = rayMarch(ro, rd, MIN_DIST, MAX_DIST); // closest object
if (co.sd > MAX_DIST) {
col = backgroundColor; // ray didn't hit anything
} else {
vec3 p = ro + rd * co.sd; // point on cube or floor we discovered from ray marching
vec3 normal = calcNormal(p);
// check material ID
if( co.id == 1 ) // floor
{
col = co.col;
} else {
// lighting
vec3 lightPosition = vec3(2, 2, 7);
vec3 lightDirection = normalize(lightPosition - p);
// color
float dif = clamp(dot(normal, lightDirection), 0.3, 1.); // diffuse reflection
col = dif * co.col + backgroundColor * .2; // Add a bit of background color to the diffuse color
}
}
// Output to screen
fragColor = vec4(col, 1.0);
}
结论
在本教程中,我们学习了如何在六个自由度上移动摄像机。我们学习了如何沿 x 轴、y 轴和 z 轴平移摄像机。我们还学习了如何使用旋转矩阵来应用偏航、俯仰和滚动,以便控制摄像机的倾斜度。利用您今天学到的知识,您可以在 Shadertoy 中调试 3D 场景并制作有趣的动画。